Ensembles
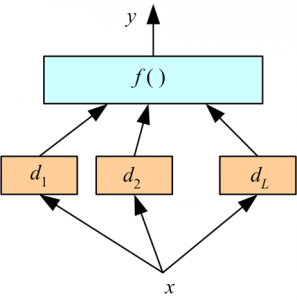
Models which are combinations of other models are called an ensemble. The simplest way to combine several classifiers is by averaging their predictions.
For example, if you have three models and four classes, you might get predictions like this:
model 1(x1) = [0.1, 0.5, 0.3, 0.1],
model 2(x1) = [0.5, 0.3, 0.1, 0.1],
model 3(x1) = [0.4, 0.4, 0.1, 0.1]
the ensemble predicts \[\left [\frac{0.1+0.5+0.4}{3}, \frac{0.5+0.3+0.4}{3}, \frac{0.4+0.2+0.2}{3}, \frac{0.1+0.1+0.1}{3} \right] \approx \left [0.3, 0.4, 0.2, 0.1 \right ]\]
for $x_1$.
Note that this is different from pluarlity voting (PV) where every model gives only one vote for the most likely class. In the case from above, it would be
model 1(x1) = [0, 1, 0, 0],
model 2(x1) = [1, 0, 0, 0],
model 3(x1) = [1, 0, 0, 0] # tie - lets just take the first
So the plurality voting ensemble would predict class 1, whereas the average probability ensemble predicts class 2. This comes from the fact that everybody might have different first choices, but they might agree on the second choice.
Please note that a tie in the predictions of a classifier with less than 100 classes is unlikely due to the higher precision of floating point numbers. However, a tie in votes can happen.
This gives you about +2 percentage points in accuracy.
Tiny Experiment on CIFAR 100
I’ve just tried this with three (almost identical) models for CIFAR 100 (https://www.cs.toronto.edu/~kriz/cifar.html). All of them were trained with Adam (https://arxiv.org/abs/1412.6980) with the same training data (the same batches). Model 1 and model 3 only differed in the second-last layer (one uses ReLU, the other tanh), model 1 and model 2 only differed in the border mode for one convolutional layer (valid vs same).
The accuracies of the single models were:
model 1: 57.02
model 2: 61.85
model 3: 48.59
The ensemble accuracy is 62.98%. Hence the ensemble is 1.13 percentage points better than the best single model!
Although I have read things like this before, it is the first time I actually tried it myself.
Ensemble Techniques
All three are so-called “meta-algorithms”: approaches to combine several machine learning techniques into one predictive model in order to decrease the variance (bagging), bias (boosting) or improving the predictive force (stacking alias ensemble).
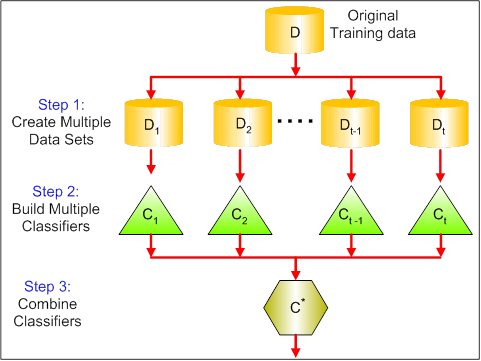
Every algorithm consists of two steps:
- Producing a distribution of simple ML models on subsets of the original data.
- Combining the distribution into one “aggregated” model.
Here is a short description of all three methods:
Bagging (stands for Bootstrap Aggregating) is a way to decrease the variance of your prediction by generating additional data for training from your original dataset using combinations with repetitions to produce multisets of the same cardinality/size as your original data. By increasing the size of your training set you can’t improve the model predictive force, but just decrease the variance, narrowly tuning the prediction to expected outcome.
Bagging tries to implement similar learners on small sample populations and then takes a mean of all the predictions. In generalized bagging, you can use different learners on different population. As you can expect this helps us to reduce the variance error.
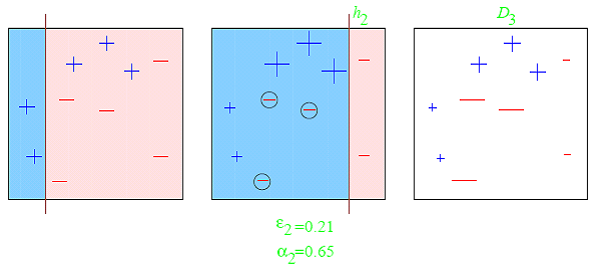
Boosting is a two-step approach, where one first uses subsets of the original data to produce a series of averagely performing models and then “boosts” their performance by combining them together using a particular cost function (=majority vote). Unlike bagging, in the classical boosting the subset creation is not random and depends upon the performance of the previous models: every new subsets contains the elements that were (likely to be) misclassified by previous models.
Boosting is an iterative technique which adjust the weight of an observation based on the last classification. If an observation was classified incorrectly, it tries to increase the weight of this observation and vice versa. Boosting in general decreases the bias error and builds strong predictive models. However, they may sometimes over fit on the training data
Stacking is a similar to boosting: you also apply several models to your original data. The difference here is, however, that you don’t have just an empirical formula for your weight function, rather you introduce a meta-level and use another model/approach to estimate the input together with outputs of every model to estimate the weights or, in other words, to determine what models perform well and what badly given these input data.
This is a very interesting way of combining models. Here we use a learner to combine output from different learners. This can lead to decrease in either bias or variance error depending on the combining learner we use.
Here is a comparison table:
Bagging Boosting Stacking Partitioning of the data into subsets Random Giving mis-classified samples higher preference Various Goal to achieve Minimize variance Increase predictive force Both Methods where this is used Random subspace Gradient descent Blending Function to combine single models (Weighted) average Weighted majority vote Logistic Regression Example Algorithm Bagged Decision Trees, Random Forest and Extra Trees AdaBoost and Stochastic Gradient Boosting - As you see, these all are different approaches to combine several models into a better one, and there is no single winner here: everything depends upon your domain and what you’re going to do. You can still treat stacking as a sort of more advances boosting, however, the difficulty of finding a good approach for your meta-level makes it difficult to apply this approach in practice.