Selain Accuracy ada Recall dan Precision

Apakah kamu yakin jika ada seseorang menciptakan model tentang mengidentifikasi teroris yang mencoba masuk ke bandara dengan accuracy lebih dari 99%? Misalkan kita ambil contoh kasus teroris, modelnya: cukup beri label setiap orang yang terbang dari seluruh bandara yang bukan teroris. Mengingat 800 juta penumpang rata-rata pada data penerbangan per tahun dan 19 orang (misalnya dikonfirmasi) sebagai teroris yang menaiki pesawat terbang dari tahun 2000-2017, model ini mencapai ketepatan yang luar biasa dari 99.9999999%! Itu mungkin terdengar mengesankan, tapi saya curiga pemerintah tidak akan menelepon sesegera mungkin untuk membeli model ini. Sementara model ini memiliki akurasi yang hampir sempurna, masalahnya adalah accuracynya jelas bukan metric yang sesuai dengan contoh kasus tersebut!

Tugas pendeteksian teroris adalah masalah klasifikasi yang tidak seimbang (imbalance): dari kasus tersebut kita memiliki dua kelas yang perlu diidentifikasi (teroris dan bukan teroris) dengan satu kategori mewakili sebagian besar data point. Masalah klasifikasi yang tidak seimbang lainnya terjadi pada pendeteksian penyakit saat tingkat penyakit di masyarakat sangat rendah. Dalam kedua kasus ini kelas positif (penyakit atau teroris) sangat kalah jumlah dengan kelas negatif. Jenis masalah ini adalah contoh kasus yang cukup umum dalam data science saat accuracy bukanlah ukuran yang baik untuk menilai kinerja dalam kasus tersebut.

Secara intuitif, kita tahu bahwa merepresentasikan semua data point sebagai hal negatif dalam masalah pendeteksian teroris hasilnya tidak cukup membantu, dan sebaliknya, kita harus fokus untuk mengidentifikasi kasus positif tersebut. Metric yang sesuai untuk memaksimalkannya dikenal dalam statistik seperti recall, atau kemampuan model untuk menemukan semua kasus yang relevan dalam dataset. Definisi recall yang tepat adalah jumlah true positive dibagi dengan jumlah true positive ditambah jumlah false negative. True positive adalah titik data yang tergolong positif dengan model yang sebenarnya bersifat positif (artinya memang benar), dan false negative adalah data point yang diidentifikasi model sebagai negatif yang sebenarnya bersifat positif (tidak benar). Dalam kasus terorisme, true positive diidentifikasi dengan teroris yang sesungguhnya, dan false negative mengartikan individu yang menjadi label bukan teroris yang sebenarnya adalah teroris. Recall dapat dianggap sebagai kemampuan model untuk menemukan semua data point yang relevan dalam dataset. \[recall = \frac{true positives}{true positives+false negatives}\] \[recall = \frac{teroris teridentifikasi dengan benar}{teroris teridentifikasi dengan benar+teroris dinyatakan bukan teroris}\]

Perhatikan pertanyaan berikut ini: jika kita memberi label pada semua individu sebagai teroris, maka recall bernilai 1.0! Jadi kita punya model classifier yang sempurna bukan? Bukan. Seperti kebanyakan konsep dalam data science, ada trade-off dalam metric yang kita pilih. Dalam kasus recall, ketika kita meningkatkan recall, kita menurunkan precision. Sekali lagi, secara intuitif kita tahu bahwa model yang memberi label 100% penumpang sebagai teroris mungkin tidak berguna karena kita harus melarang setiap orang untuk terbang menggunakan pesawat. Statistik memberi kita alasan untuk mengungkapkan intuisi kita: model baru ini akan mengalami precision rendah, atau kemampuan model klasifikasi untuk mengidentifikasi hanya pada data point yang relevan.

Precision didefinisikan sebagai jumlah true positive dibagi dengan jumlah true positive ditambah jumlah false positive. False positive adalah kasus yang hasil dari modelnya salah, label positif yang sebenarnya negatif, atau dalam contoh kita, individu yang digolongkan oleh model sebagai teroris yang sebenarnya bukan teroris. Sementara recall adalah kemampuan untuk menemukan semua contoh yang relevan dalam dataset, precision mengungkapkan proporsi data point yang menurut model kita relevan dengan yang sebenarnya relevan. \[precision = \frac{true positives}{true positives+false positives}\] \[precision = \frac{teroris teridentifikasi dengan benar}{teroris teridentifikasi dengan_benar+bukan teroris dinyatakan sebagai teroris}\]

Sekarang, kita dapat melihat bahwa model pertama kita yang memberi label kepada semua individu sebagai bukan teroris tidak terlalu berguna. Meski memiliki accuracy hampir sempurna, ia memiliki 0 precision dan 0 recall karena tidak ada yang true positive! Misalkan kita memodifikasi model sedikit aja, dan mengidentifikasi satu individu dengan benar sebagai teroris. Sekarang, nilai precision akan menjadi 1.0 (bukan false positive) tapi recall akan menjadi sangat rendah karena kita masih memiliki banyak false negative. Misal lebih esktrem lagi jika mengklasifikasikan semua penumpang sebagai teroris, kita akan memiliki recall 1.0 (kita akan menangkap setiap teroris) namun precision akan sangat rendah dan kita akan menahan banyak individu yang tidak bersalah. Dengan kata lain, saat kita meningkatkan precision akan mengurangi recall dan sebaliknya

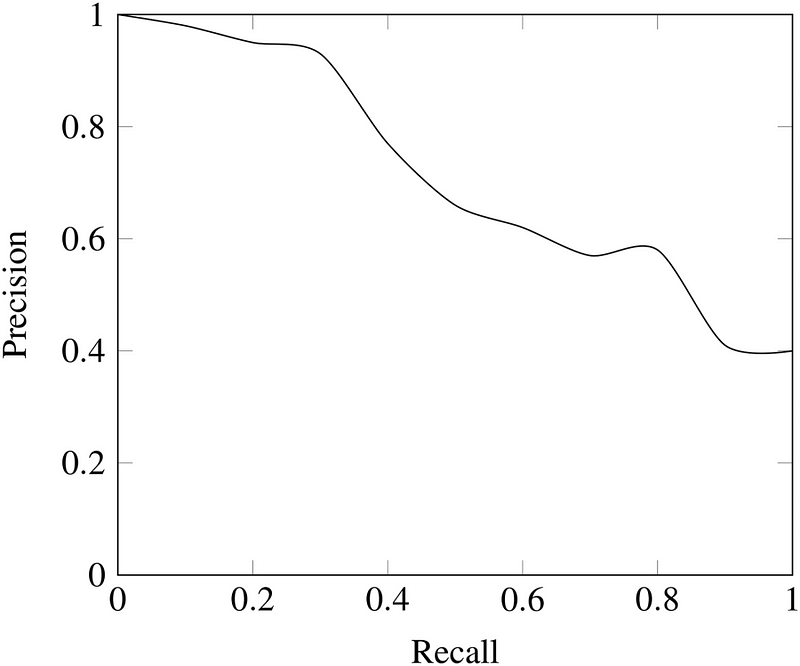
Menggabungkan Precision dan Recall

Dalam beberapa situasi, kita mungkin tahu bahwa kita ingin memaksimalkan recall atau precision dengan mengorbankan metric lainnya. Misalnya, dalam skrining penyakit awal pasien untuk pemeriksaan lanjutan, kita mungkin menginginkan recall kembali mendekati 1.0 (kita ingin menemukan semua pasien yang benar-benar memiliki penyakit) dan kita dapat menerima precision rendah jika biaya follow-up pemeriksaan tidak signifikan. Namun, dalam kasus dimana kita ingin menemukan perpaduan precision dan recall yang optimal, kita dapat menggabungkan dua metric tersebut dengan menggunakan apa yang disebut F1 Score.

F1 Score adalah rata-rata dari precision dan recall yang memperhitungkan kedua metrik tersebut dalam persamaan berikut: \[F_1 = 2 * \frac{precision * recall}{precision + recall}\]

Kita menggunakan harmonic mean (bukan rata-rata sederhana karena akan menghukum nilai ekstrim). Pengelompokan dengan precision 1.0 dan recall 0.0 memiliki rata-rata 0.5 sederhana namun F1 Score bernilai 0. F1 Score memberikan bobot yang sama untuk kedua ukuran tersebut dan merupakan contoh spesifik dari metode metric Fβ dimana β dapat disesuaikan dengan memberi bobot lebih pada recall atau precision. (Ada metric lain untuk menggabungkan precision dan recall, seperti Geometris Mean dari recall dan precision, namun F1 Score adalah yang paling umum digunakan) Jika kita ingin membuat model klasifikasi dengan keseimbangan recall dan precision secara optimal, maka kita mencoba memaksimalkan F1 Score.

Teknik Visualisasi Precision dan Recall

Sampai sini kita sudah belajar beberapa istilah baru dan kita akan menggunakan sebuah contoh untuk menunjukkan bagaimana penggunaannya dengan praktik lebih lanjut. Sebelum kita bisa ke sana kita perlu secara singkat membicarakan konsep yang digunakan untuk menunjukkan precision dan recall. Pertama adalah confusion matrix (http://www.dataschool.io/simple-guide-to-confusion-matrix-terminology/) yang berguna untuk menghitung precision dan recall dengan cepat dari label hasil prediksi suatu model. Confusion Matrix untuk klasifikasi biner menunjukkan empat hasil yang berbeda: true positive, false positive, true negative, dan false negative. Nilai sebenarnya berupa kolom, dan nilai prediksi (label) membentuk baris. Perpotongan dari baris dan kolom menunjukkan salah satu dari empat hasil. Misalnya, jika kita memprediksi data point yang positif, tapi sebenarnya negatif, ini adalah false negative.

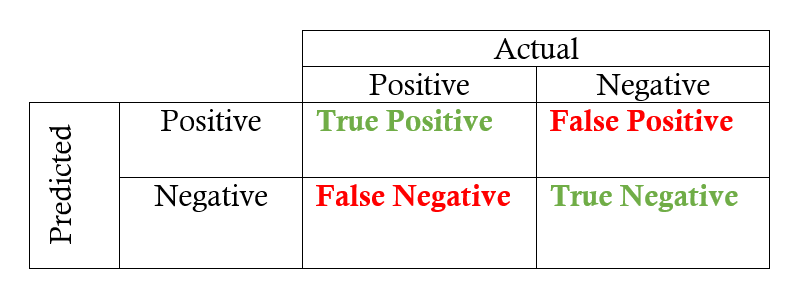
Dari confusion matrix ke recall dan precision memerlukan nilai masing-masing dalam matriks dan menerapkan persamaan berikut: \[recall = \frac{true positives}{true positives + false negatives}\] \[precision = \frac{true positives}{true positives + false positives}\]

Teknik visualisasi utama lainnya untuk menunjukkan kinerja model klasifikasi adalah kurva Receiver Operating Characteristic (ROC) (http://scikit-learn.org/stable/auto_examples/model_selection/plot_roc.html). Jangan takut karena melihat namanya agak rumit! Idenya relatif sederhana: kurva ROC menunjukkan bagaimana perubahan hubungan recall vs precision saat kita mengubah threshold untuk mengidentifikasi kelas positif pada model kita. Threshold mewakili nilai titik data yang dipertimbangkan di kelas positif. Jika kita memiliki model untuk mengidentifikasi suatu penyakit, model kita mungkin menghasilkan skor untuk setiap pasien antara 0 dan 1 dan kita dapat menetapkan threshold dalam kisaran ini untuk memberi label pada pasien yang memiliki penyakit (label positif). Dengan mengubah threshold, kita dapat mencoba untuk mencapai keseimbangan antara precision vs recall yang tepat.

Kurva ROC menggambarkan tingkat true positive pada sumbu y dibandingkan tingkat false positive pada sumbu x. True Positive Rate (TPR) adalah recall dan False Positive Rate (FPR) adalah probabilitas dari false alarm. Kedua hal ini dapat dihitung dari confusion matrix berikut \[true positive rate = \frac{true positives}{true positives + false negatives}\] \[false positive rate = \frac{true positives}{true positives + false positives}\]

Kurva ROC digambarkan sebagai berikut:

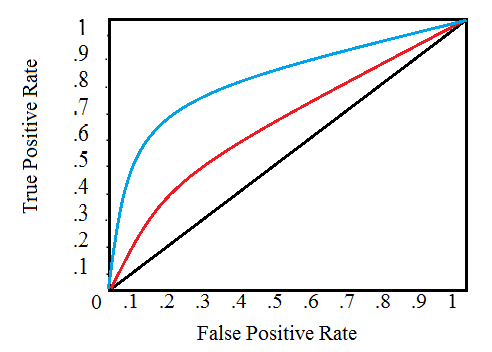
Garis diagonal hitam menunjukkan random classifier, kurva merah dan biru menunjukkan dua model klasifikasi yang berbeda. Untuk model tertentu, kita hanya bisa bertahan pada satu kurva, tapi kita bisa bergerak sepanjang kurva dengan menyesuaikan threshold kita untuk mengklasifikasikan kasus positif. Umumnya, saat menurunkan threshold, kita bergerak ke kanan dan ke atas sepanjang kurva. Dengan threshold 1.0, kita akan berada di kiri bawah grafik karena kita tidak mengidentifikasi data point sebagai kelas positif yang mengarah ke bukan true positive dan bukan true negative (TPR = FPR = 0). Ketika kita menurunkan threshold, kita mengidentifikasi lebih banyak data point sebagai kelas positif, mengarah ke true positive, tetapi banyak juga ke true negative (TPR dan FPR meningkat). Akhirnya, pada threshold 0.0, kita mengidentifikasi semua data point sebagai kelas positif dan menemukannya berada di sudut kanan atas kurva ROC (TPR = FPR = 1.0).

Rekap

Kita sudah membahas beberapa istilah diatas, tidak ada yang sulit sebenarnya jika sendiri-sendiri, tapi gabungannya bisa sedikit puyeng! Mari kita rekap dan coba dengan sebuah contoh

• Empat output dari Binary Classification
  1. True positives: data points diberi label positif yang memang sebenarnya bernilai positif
  2. False positives: data points diberi label positif yang sebenarnya bernilai negatif
  3. True negatives: data points diberi label negatif yang memang sebenarnya bernilai negatif
  4. False negatives: data points diberi label negatif yang sebenarnya bernilai positif
• Matric Recall and Precision
  1. Recall: nilai dari sebuah model klasifikasi untuk mengidentifikasi semua instance yang relevan
  2. Precision: nilai dari sebuah model klasifikasi untuk mengembalikan hanya instance yang relevan
  3. F1 Score: Metric yang mengkombinasikan recall and precision menggunakan harmonic mean
• Visualisasi Recall and Precision Teknik
  1. Confusion matrix: menunjukan label actual dan predicted dari masalah klasifikasi
  2. Receiver operating characteristic (ROC) curve: kurva tentang true positive rate (TPR) vs the false positive rate (FPR) sebagai fungsi threshold dari sebuah model untuk mengklasifikasikan kelas positif
  3. Area under the curve (AUC): Matric untuk mengkalkulasi perfoma secara keseluruhan dari model klasifikasi berdasarkan area di bawah kurva ROC

Contoh Implementasi

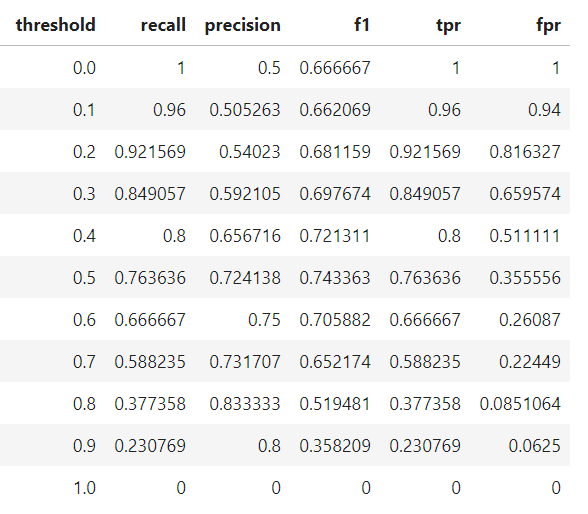
Tugas kita adalah mendiagnosis 100 pasien dengan penyakit yang ada pada 50% populasi umum. Kita akan mengasumsikan model black box, di mana kita memasukkan informasi tentang pasien dan mendapat skor antara 0 dan 1. Kita dapat mengubah threshold untuk memberi label pasien sebagai positif (memiliki penyakit) untuk memaksimalkan kinerja pengklasifikasian. Kita akan mengevaluasi threshold dari 0.0 menjadi 1.0 dengan penambahan 0.1, pada setiap langkah yang menghitung precision, recall, F1 score, dan lokasi pada kurva ROC. Berikut adalah hasil klasifikasi di setiap thresholdnya:

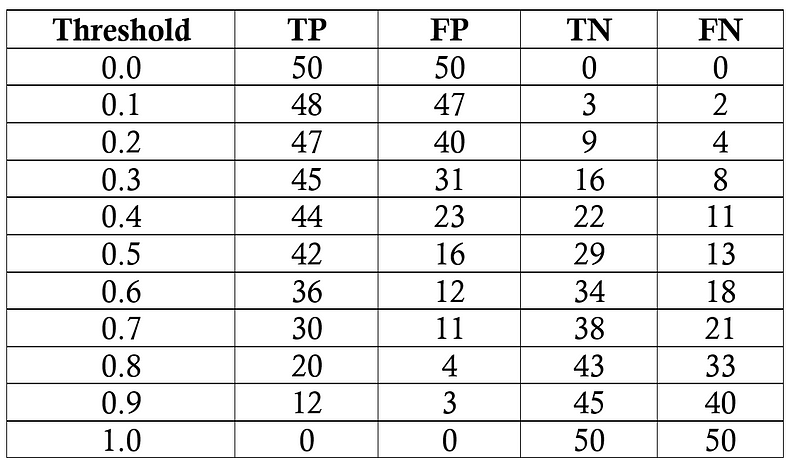
Kita akan melakukan satu contoh perhitungan recall, precision, true positive rate, dan false positive rate pada threshold 0.5. Pertama kita membuat confusion matrix:

Kita bisa menggunakan angka di dalam matriks tersebut untuk menghitung recall, precision, dan F1 score: \[recall = \frac{TP}{TP + FN} = \frac{42}{42 + 13} = 0.76\] \[precision = \frac{TP}{TP + FP} = \frac{42}{42 + 16} = 0.724\] \[F1 Score = 2 * \frac{precision * recall}{precision + recall} = 0.74\]

Kemudian kita hitung tingkat true positif dan false negative rate untuk menemukan koordinat y dan x untuk kurva ROC. \[true positive rate = \frac{TP}{TP + FN} = \frac{42}{42 + 13} = 0.76\] \[false positive rate = \frac{FP}{FP + TN} = \frac{16}{16 + 29} = 0.36\]

Untuk membuat keseluruhan kurva ROC, kita melakukan proses ini di setiap threshold. Seperti yang mungkin kamu pikirin, ini sangat membosankan, jadi alih-alih melakukannya dengan tangan, kami menggunakan bahasa seperti Python untuk melakukannya! Tersedia Notebook Jupyter dengan perhitungannya ada di GitHub agar kamu bisa melihat implementasinya. Kurva ROC terakhir ditunjukkan di bawah ini dengan diatas data pointnya.

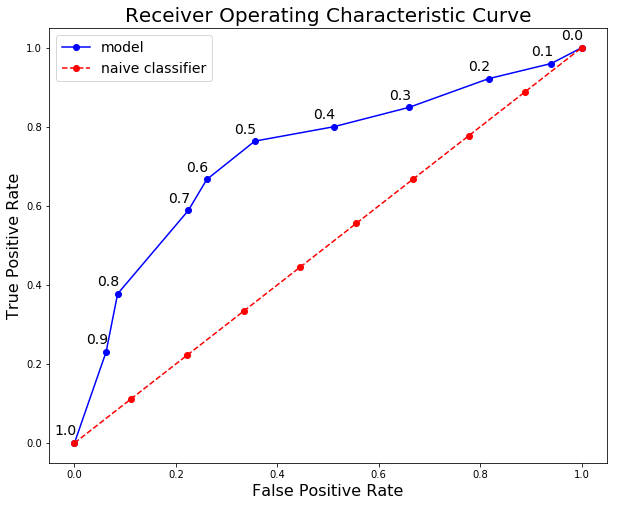
Di sini kita bisa melihat semua konsep secara bersamaan! Pada threshold 1.0, kita mengklasifikasikan tidak ada pasien yang memiliki penyakit ini dan karenanya memiliki recall dan precision 0.0. Seiring threshold menurun, recall kembali meningkat karena kita mengidentifikasi lebih banyak pasien yang memiliki penyakit. Namun, saat recall kita meningkat, precision kita menurun karena selain meningkatkan true positive, kita meningkatkan false positive. Pada threshold 0.0, recall kita terlihat sempurna (kita menemukan semua pasien dengan penyakit ini) namun precision kita rendah karena kita memiliki banyak false positive. Kita dapat bergerak sepanjang kurva untuk model tertentu dengan mengubah threshold dan memilih threshold yang memaksimalkan F1 Score. Untuk menggeser keseluruhan kurva, kita perlu membangun model yang berbeda. Berikut adalah statistik dari model akhir di setiap threshold:

Kesimpulan

Kita cenderung menggunakan accuracy karena setiap orang lebih familiar dengan hal tersebut! Meskipun ada metrik yang lebih sesuai seperti recall dan precision,sekarang kita sudah memiliki pengertian intuitif mengapa mereka bekerja lebih baik untuk beberapa kasus seperti klasifikasi yang tidak seimbang (imbalance). Statistik memberi kita definisi dan persamaan matematika untuk menghitung metric ini. Data Science adalah tentang mencari tools yang tepat untuk digunakan untuk pekerjaan sesuai, dan seringkali kita perlu melampaui accuracy saat mengembangkan model klasifikasi. Mengetahui tentang recall, precision, F1 score, dan kurva ROC memungkinkan kita untuk menilai model klasifikasi dan harus membuat kita berpikir skeptis tentang siapa yang hanya memuji accuracy suatu model, terutama untuk masalah yang tidak seimbang (imbalance). Seperti yang telah kita lihat, accuracy tidak memberikan penilaian yang berguna mengenai beberapa masalah tertentu, namun sekarang kita tahu bagaimana menerapkan metric dengan lebih baik! .