1. Setup Eksperiment
Kita akan melakukan A/B Test untuk suatu company yang mencoba meningkatkan jumlah pengguna yang mendaftar untuk akun premium. Tujuan A/B Test adalah untuk mengevaluasi apakah sebuah perubahan tertentu pada website akan menghasilkan peningkatan kinerja dalam metrik tertentu. Kita boleh memutuskan untuk test alternatif yang sangat sederhana seperti mengubah tampilan satu tombol pada halaman web atau menguji layout dan judul yang berbeda. Kita juga bisa menjalankan A/B Test pada proses multi-step yang mungkin memiliki banyak perbedaan. Contoh langkah-langkah yang diperlukan dalam mendaftar pada pengguna baru atau proses melakukan pembelian pada online marketplace. A/B Test adalah subject yang cukup penting dan ada banyak teknik serta aturan untuk menyiapkan sebuah eksperiment. Kita akan membuatnya lebih sederhana agar kita bisa fokus pada matematikanya.
Baseline Conversion Rate and Lift
Sebelum menjalankan test, kita perlu mengetahui baseline conversion rate dan lift yang diinginkan atau peningkatan sign-up yang ingin kita test. Baseline conversion rate adalah rate sekarang dimana kita mendaftarkan pengguna baru dengan desain yang sudah ada. Contoh, kita akan melakukan test untuk mengkonfirmasi bahwa perubahan yang kita lakukan pada proses pendaftaran, akan menghasilkan setidaknya 2% peningkatan pada sign-up rate. Saat ini kita cuma punya 10 dari 100 pengguna yang ditawari akun premium.
bcr = 0.10 # baseline conversion rate
d_hat = 0.02 # perbedaan antara kedua grup
Grup Kontrol (A) dan Grup test (B)
Biasanya, jumlah total pengguna yang berpartisipasi dalam A/B Test merupakan persentase kecil dari jumlah total pengguna. Pengguna dipilih secara acak dan ditetapkan ke grup kontrol atau grup test.
Awalnya, kita akan mengumpulkan 1000 pengguna untuk setiap grup dan melakukan treatment dengan halaman pendaftaran saat ini ke grup kontrol dan halaman pendaftaran baru ke grup test.
# A is control; B is test
N_A = 1000
N_B = 1000
Significance level dan Statistical Power
Kita akan menetapkan Significance Level pada 0,05 dan Statistical Power yang kita inginkan menjadi 0,80. Kita bisa menjadikan tingkat significance level sebagai probabilitas bahwa test yang kita lakukan akan menghasilkan false positive. False positive adalah ketika kita salah memasukkan bahwa desain baru lebih baik. Nilai ini di set kecil karena kita ingin membatasi nilai probabilitasnya. Statistical Power dapat digambarkan sebagai probabilitas bahwa test yang kita lakukan akan menghasilkan true positif. Jika desain baru memang benar-benar lebih baik, kita ingin eksperiment yang kita lakukan menunjukkan bahwa ada probabilitas setidaknya 80%. Parameter ini biasanya ditetapkan pada 0,05 dan 0,80, ketika kita pertama kali setup sebuah experiment.
2. Run Test
Karena ini hipotesis, kita perlu data “dummy” sebagai contoh kasus. ada fungsi untuk generate data dummy:
import scipy.stats as scs
import pandas as pd
# import numpy as np
def generate_data(N_A, N_B, p_A, p_B, days=None, control_label='A',
test_label='B'):
"""Returns a pandas dataframe with fake CTR data
Example:
Parameters:
N_A (int): sample size for control group
N_B (int): sample size for test group
Note: final sample size may not match N_A provided because the
group at each row is chosen at random (50/50).
p_A (float): conversion rate; conversion rate of control group
p_B (float): conversion rate; conversion rate of test group
days (int): optional; if provided, a column for 'ts' will be included
to divide the data in chunks of time
Note: overflow data will be included in an extra day
control_label (str)
test_label (str)
Returns:
df (df)
"""
# initiate empty container
data = []
# total amount of rows in the data
N = N_A + N_B
group_bern = scs.bernoulli(0.5)
# initiate bernoulli distributions to randomly sample from
A_bern = scs.bernoulli(p_A)
B_bern = scs.bernoulli(p_B)
for idx in range(N):
# initite empty row
row = {}
# for 'ts' column
if days is not None:
if type(days) == int:
row['ts'] = idx // (N // days)
else:
raise ValueError("Provide an integer for the days parameter.")
# assign group based on 50/50 probability
row['group'] = group_bern.rvs()
if row['group'] == 0:
# assign conversion based on provided parameters
row['converted'] = A_bern.rvs()
else:
row['converted'] = B_bern.rvs()
# collect row into data container
data.append(row)
# convert data into pandas dataframe
df = pd.DataFrame(data)
# transform group labels of 0s and 1s to user-defined group labels
df['group'] = df['group'].apply(
lambda x: control_label if x == 0 else test_label)
return df
dengan menggunakan code berikut:
ab_data = generate_data(N_A, N_B, bcr, d_hat)
Fungsi generate_data menghasilkan tabel berikut. Hanya lima baris pertama yang ditampilkan. Kolom converted menunjukkan apakah pengguna mendaftar untuk layanan premium atau tidak dengan 1 atau 0. Grup ini akan menjadi grup test.
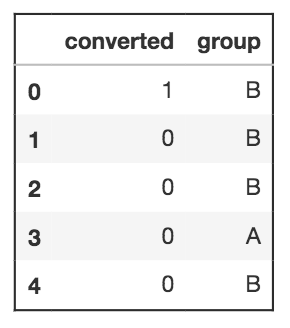
Sekarang kita lihat summarynya menggunakan pivot table pada pandas:
ab_summary = ab_data.pivot_table(values='converted',
index='group',
aggfunc=np.sum)
# add additional columns to the pivot table
ab_summary['total'] = ab_data.pivot_table(values='converted',
index='group',
aggfunc=lambda x: len(x))
ab_summary['rate'] = ab_data.pivot_table(values='converted',
index='group')
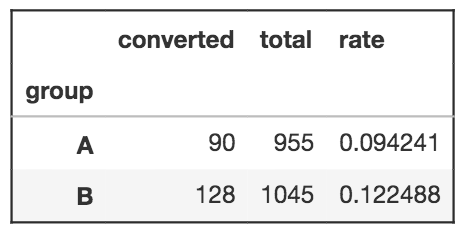
Kelihatannya perbedaan dalam conversion rates antara kedua grup adalah 0,028 yang lebih besar dari lift yang awalnya kita inginkan sebesar 0,02. Ini pertanda baik tapi hal ini tidak cukup confident untuk desain yang baru. Pada titik ini kita belum mengukur seberapa yakin dengan hasil yang didapat. Hal ini dapat diperjelas dengan melihat distribusi dari kedua grup.
3. Membandingkan Dua Grup
P-Value
Kita bisa membandingkan kedua grup dengan memplot distribusi grup control dan menghitung probabilitas hasil dari grup test. Kita bisa mengasumsikan bahwa distribusi untuk grup control adalah distribusi binomial karena data yang kita ambil merupakan serangkaian percobaan Bernoulli, dimana setiap percobaan hanya memiliki dua hasil yang mungkin terjadi (mirip dengan lempar koin).
fig, ax = plt.subplots(figsize=(12,6))
x = np.linspace(A_converted-49, A_converted+50, 100)
y = scs.binom(A_total, A_cr).pmf(x)
ax.scatter(x, y, s=10)
ax.axvline(x=B_cr * A_total, c='blue', alpha=0.75, linestyle='--')
plt.xlabel('converted')
plt.ylabel('probability')
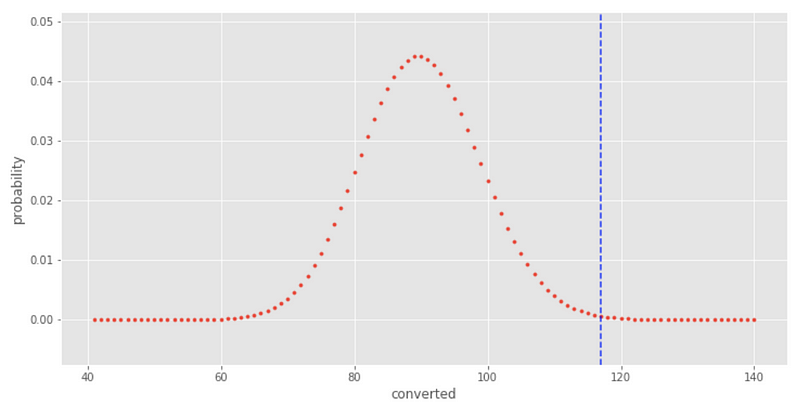
Distribusi untuk grup control ditampilkan dalam warna merah dan hasil dari grup test ditunjukkan oleh garis putus-putus biru. Kita bisa lihat bahwa hasil probabilitas dari grup test sangat rendah. Probabilitas ini disebut p-value dan 0,00085 untuk eksperiment kita saat ini. Ini jauh lebih sedikit daripada tingkat signifikansi yang kita tetapkan pada 0,05 dan menunjukkan bahwa desain baru kita sangat efektif. Namun, p-value tidak menunjukkan tingkat kepercayaan dari hasil tersebut. Mari juga plot grup test sebagai distribusi binomial dan bandingkan distribusinya satu sama lain.
fig, ax = plt.subplots(figsize=(12,6))
xA = np.linspace(A_converted-49, A_converted+50, 100)
yA = scs.binom(A_total, p_A).pmf(xA)
ax.scatter(xA, yA, s=10)
xB = np.linspace(B_converted-49, B_converted+50, 100)
yB = scs.binom(B_total, p_B).pmf(xB)
ax.scatter(xB, yB, s=10)
plt.xlabel('converted')
plt.ylabel('probability')
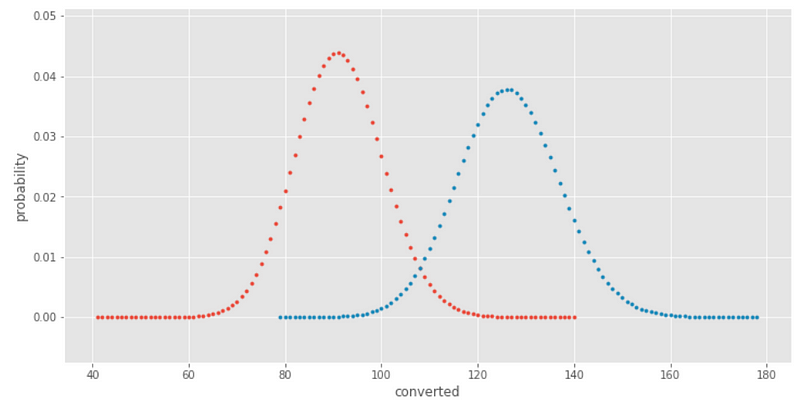
Kita bisa melihat bahwa grup test mengkonversi lebih banyak pengguna daripada grup kontrol. Namun, kita ingin fokus pada conversion rate dari dua grup tersebut. Untuk menghitung ini, kita perlu standarisasi data dan membandingkan nilai probabilitas suksesnya, p, untuk setiap grup.
Distribusi Bernoulli dan Central Limit Theorem
Coba kita perhatikan distribusi Bernoulli untuk grup control.
\(X \sim Bernoulli(p)\) di mana p adalah probabilitas konversi dari grup control.
Menurut sifat distribusi Bernoulli, mean dan varians adalah sebagai berikut: \[E(X) = p\] \[Var(X)=p(1-p)\]
Menurut teorema limit pusat, dengan menghitung banyak sampel berarti kita dapat mendekati mean sebenarnya dari populasi, 𝜇, dari data mana untuk grup kontrol diambil. Distribusi sampel, p, akan terdistribusi secara normal di sekitar mean yang sebenarnya dengan standar deviasi sama dengan standar error dari mean. Persamaan untuk ini diberikan sebagai: \[\sigma_{\bar x} = \frac{s}{\sqrt{n}} = \frac{\sqrt{p(1-p)}}{\sqrt{p}}\]
Maka, kita bisa menganggap kedua grup sebagai distribusi normal dengan properti berikut: \[\hat p \sim Normal \Bigg(\mu=p, \sigma = \frac{\sqrt{p(1-p)}}{\sqrt{p}}\Bigg)\]
Hal yang sama juga dilakukan untuk kelompok test. Jadi, kita bisa memiliki dua distribusi normal untuk p_A dan p_B.
# standard error of the mean for both groups
SE_A = np.sqrt(p_A * (1-p_A)) / np.sqrt(A_total)
SE_B = np.sqrt(p_B * (1-p_B)) / np.sqrt(B_total)
# plot the null and alternate hypothesis
fig, ax = plt.subplots(figsize=(12,6))
x = np.linspace(0, .2, 1000)
yA = scs.norm(p_A, SE_A).pdf(x)
ax.plot(xA, yA)
ax.axvline(x=p_A, c='red', alpha=0.5, linestyle='--')
yB = scs.norm(p_B, SE_B).pdf(x)
ax.plot(xB, yB)
ax.axvline(x=p_B, c='blue', alpha=0.5, linestyle='--')
plt.xlabel('Converted Proportion')
plt.ylabel('PDF')
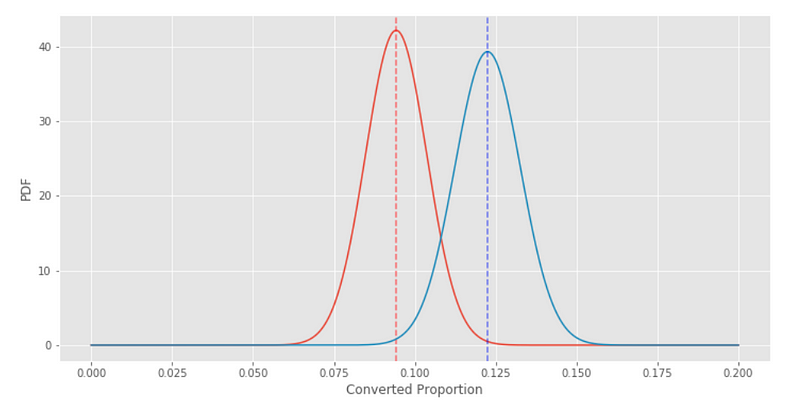
Garis putus-putus menunjukkan tingkat konversi rata-rata conversion rate untuk setiap grup. Jarak antara garis putus-putus merah dan garis putus-putus biru sama dengan perbedaan rata-rata antara grup kontrol dan grup test. d_hat adalah distribusi perbedaan antara variabel acak dari dua kelompok tersebut. \[\hat d = \hat p_B - \hat p_A\]
Variance Total
Ingat bahwa hipotesis nol menyatakan bahwa perbedaan dalam probabilitas antara kedua kelompok adalah nol. Oleh karena itu, mean untuk distribusi normal ini akan menjadi nol. Properti lain yang kita perlukan untuk distribusi normal adalah standar deviasi atau variasinya. (Catatan: variansnya adalah standar deviasi kuadrat.) Varians dari perbedaannya akan tergantung pada varians dari probabilitas untuk kedua kelompok.
Properti dasar dari varians yaitu varians dari jumlah dua variabel independen acak adalah jumlah dari varians. \[Var(X + Y) = Var(X) + Var(Y)\] \[Var(X - Y) = Var(X) + Var(Y)\]
Ini artinya bahwa hipotesis nol dan hipotesis alternatif akan memiliki varian yang sama yang akan menjadi jumlah dari varians untuk grup kontrol dan grup test. \[Var(\hat d) = Var(\hat p_B - \hat p_A) = Var(\hat p_A) + Var(\hat p_B) = \frac{p_A(1-p_A)}{n_A}+\frac{p_B(1-p_B)}{n_B}\]
Simpangan baku nya dapat dihitung dengan: \[\sigma = \sqrt{Var(\hat d)} = \sqrt{\frac{p_A(1-p_A)}{n_A}+\frac{p_B(1-p_B)}{n_B}}\]
Jika kita menempatkan persamaan ini dalam standar deviasi untuk distribusi Bernoulli, $s$: \[\sigma = \sqrt{Var(\hat d)} = \sqrt{\frac{s^2_A}{n_A}+\frac{s^2_B}{n_B}}\]
dan kita mendapatkan pendekatan Satterthwaite untuk standar error gabungan. Jika kita menghitung probabilitas gabungan dan menggunakannya untuk menghitung standar deviasi untuk kedua kelompok, kita mendapatkan: \[\sigma = \sqrt{Var(\hat d)} = \sqrt{\frac{s^2_A}{n_A}+\frac{s^2_B}{n_B}} = \sqrt{s_p \bigg(\frac{1}{n_A}+\frac{1}{n_B}\bigg)} = \sqrt{\hat p_p(1-\hat p_p)\bigg(\frac{1}{n_A}+\frac{1}{n_B}\bigg)}\]
dimana: \[\hat p_p = \frac{p_A N_A + p_b N_B}{N_A+N_B}\]
Ini adalah persamaan yang sama yang digunakan di Udacity. Kedua persamaan itu untuk standar error gabungan yang akan memberikan hasil yang sangat mirip.
Dengan itu, kita sekarang memiliki informasi yang cukup untuk membangun distribusi hipotesis nol dan hipotesis alternatif.
Bandingkan Hipotesis Null vs Hipotesis Alternatif
Mari mulai dengan mendefinisikan hipotesis nol dan hipotesis alternatif.
- Hipotesis nol adalah posisi bahwa perubahan dalam desain yang dibuat untuk kelompok test akan mengakibatkan tidak ada perubahan pada conversion rate.
- Hipotesis alternatif adalah posisi yang berlawanan bahwa perubahan dalam desain untuk kelompok test akan menghasilkan peningkatan (atau pengurangan) pada conversion rate.
Kalau di Udacity, hipotesis nol akan menjadi distribusi normal dengan rata-rata nol dan standar deviasi sama dengan standar error yang dikumpulkan. \[H_0 : d = 0\] \[\hat d_0 \sim Normal(0, SE_{pool})\]
Hipotesis alternatif memiliki standar deviasi yang sama dengan hipotesis nol, tetapi mean akan terletak pada perbedaan di conversion rate-nya, d_hat. Masuk akal sih, karena kita bisa hitung selisih conversion rate-nya dari data, tapi distribusi normal mewakili kemungkinan nilai yang dapat dari hasil eksperimen ini. \[H_A:d=p_B - p_A\] \[\hat d_A \sim Normal(d, SE_{pool})\]
Sekarang kita paham derivasi dari standar error yang terkumpul, kita bisa langsung memplot hipotesis nol dan alternatif untuk eksperimen kedepannya. Berikut adalah script untuk membuat hipotesis nol dan alternatif sama abplot.
# define the parameters for abplot()
# use the actual values from the experiment for bcr and d_hat
# p_A is the conversion rate of the control group
# p_B is the conversion rate of the test group
n = N_A + N_B
bcr = p_A
d_hat = p_B - p_A
abplot(n, bcr, d_hat)
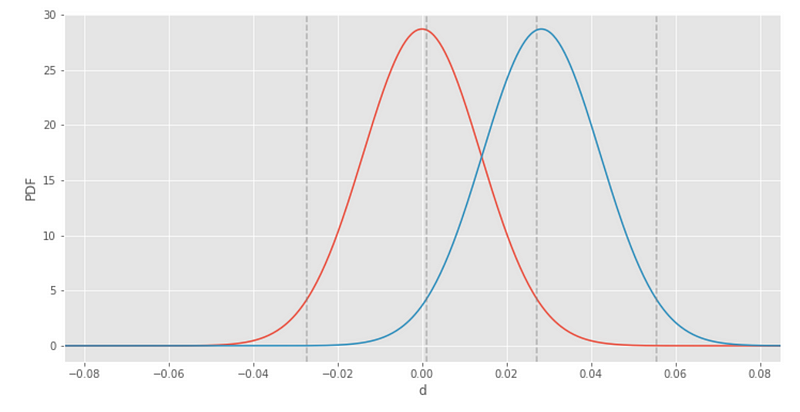
Balikan visualisasi statistical power dengan menambahkan parameter show_power=True.
abplot(n, bcr, d_hat, show_power=True)
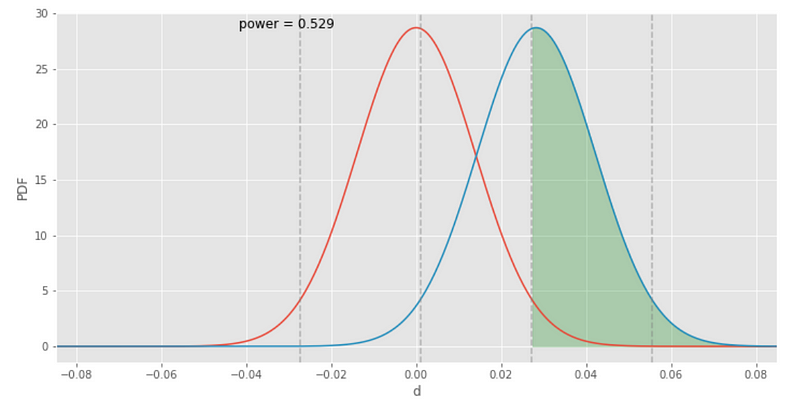
Garis putus-putus abu-abu yang di plot di atas mewakili confidence level atau significance level yang dapat digunakan untuk mengukur statistical power. Area berarsir hijau menunjukkan statistical power dan nilai terhitung juga ditampilkan di plot. Dan terlihat bahwa nilainya tidak lebih besar dari 80%. Semua evaluasi kita hingga saat ini menunjukkan bahwa perubahan dalam sebuah desain akan menghasilkan lebih banyak konversi, tapi kita tidak memiliki cukup statistical power untuk yakin bahwa hal ini akan menjadi kesimpulannya. Oleh karena itu, penting untuk membandingkan hipotesis nol dan alternatif untuk menentukan apakah ada statistical significance yang cukup.
Pada step ini, kita bisa menambahkan lebih banyak user ke grup kontrol dan test untuk membuat distribusi lebih sempit. Bisa saja membantu meningkatkan statistical power tetapi juga dapat mengartikan bahwa peningkatan yang diproyeksikan akan benar-benar lebih rendah dari 0,028, dalam hal ini statistical power tidak mungkin meningkat sama sekali. Dalam kedua kasus, kita akan semakin yakin bahwa experiment yang kita lakukan merupakan hal yang memberikan hasil yang bagus dan ga sia-sia.